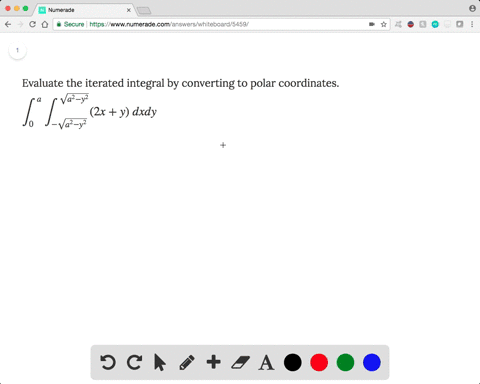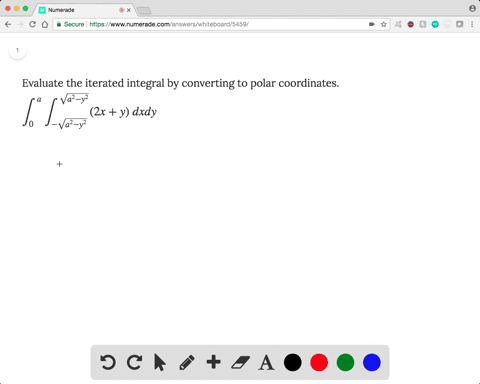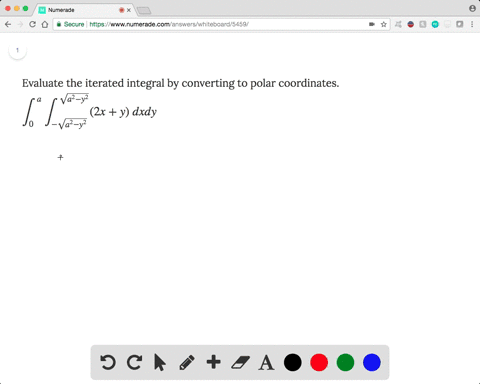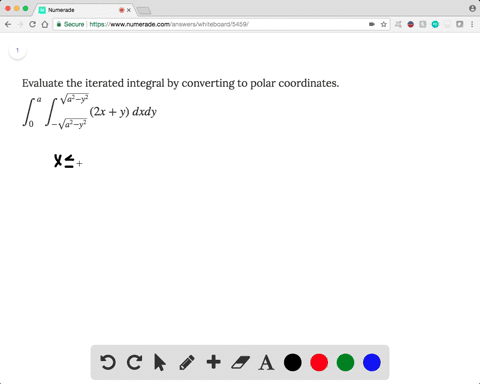
Then the double integral in polar coordinates is given by the formula ∬ R f (x,y)dxdy = β ∫ α h(θ) ∫ g(θ) f (rcosθ,rsinθ)rdrdθ The region of integration (Figure 3) is called the polar rectangle if it satisfies the following conditions 0 ≤ a ≤ r ≤ b, α ≤ θ ≤ β, where β−α ≤ 2πDouble integrals in Cartesian coordinates (Section 152) Start with the outer limits x ∈ 0,3 y 6 2 − 2x/3 and y > 2 r 1 − x2 32 The lower limit is part of the ellipse x2 32 y2 22 = 1 x2 2 y 3 Double integrals in Cartesian coordinates (Section 152)As argued above, the original integral will be twice as large as this integral It follows that ∫ 1 0 ∫ 1 0 emax(x2,y2)dydx= e−1 ∫ 0 1 ∫ 0 1 e max ( x 2, y 2) d y d x = e − 1
2
Double integral of e^max(x^2 y^2)
Double integral of e^max(x^2 y^2)-Free double integrals calculator solve double integrals stepbystep This website uses cookies to ensure you get the best experience {1y^2}dydx \int \int x^2 \int_{0}^{1}\int_{0}^{1}xy\dydx;Learning Objectives 521 Recognize when a function of two variables is integrable over a general region;
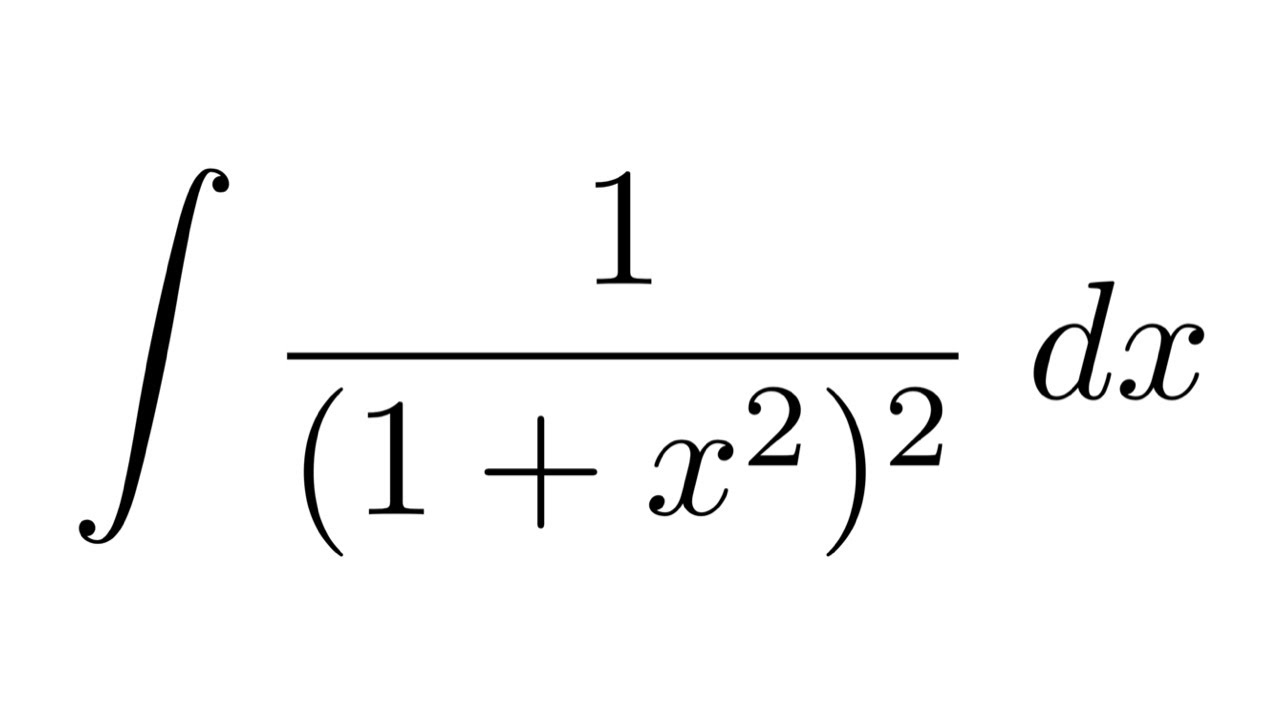



Integral Of 1 1 X 2 Substitution Youtube
Question Calculate the double integral \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1x^2}} e^{x^2y^2} \; Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any regionDouble(int(int(exp(x^2y^2),y,1x,1x^2),x,0,1)) Warning Explicit integral could not be found > In D\matlabr11\toolbox\symbolic\@sym\intm at line 58 ans = Problem 1 Evaluate the iterated integrals and We will now address the problem of determining limits for a double integral from a geometric description of the region of integration
Double Integrals over General Regions In this section we consider double integrals over more general regions Suppose that the region R is defined by G_1(x)2 Answers2 If you want to integrate over both x and y, then you can convert it to an integral in polar coordinates ∫ ∞ − ∞∫ ∞ − ∞e − ( x2 y2) dx dy = ∫ ∞ 0 ∫2π 0 e − r2 r dθ dr = 2π∫ ∞ 0 e − r2 r dr = π∫ ∞ 0 e − u du You cannot find the indefinite integral with respect to Homework Statement We define the improper integral (over the entire plane R^2) I as a double integral inf,infx inf,inf of e^ (x^2y^2)dA as equal to the lim as a> inf of the double integral under Da of e^ (x^2y^2)dA where Da is the disk with the radius a and center at the origin Show that the I (the original double integral) equals pi
In Double Integrals over Rectangular Regions, we studied the concept of double integrals and examined the tools needed to compute themWe learned techniques and properties to integrate functions of two variables over rectangular regions We also discussed several applications, such as finding the volume bounded above by a function over a rectangular region, Calling #I =int_oo^oo e^{x^2/2}dx# we know that #I^2 = (int_oo^oo e^{x^2/2}dx)(int_oo^oo e^{y^2/2}dy)# but the integrals are independent so #I^2 = int_oo^oo int_oo^oo e^{(x^2y^2)/2}dx dy# Changing to polar coordinates #rho^2 = x^2y^2# #dx dy equiv rho d rho d theta# To cover the whole plane in polar coordinates we have Evalutate double integral R, (xy)e^(x^2y^2) dA, where R is the rectangle enclosed by the lines xy=0,xy=3,xy=0 and xy=2 Best Answer
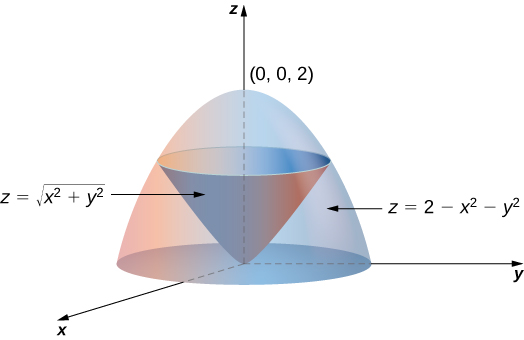



Triple Integrals In Cylindrical And Spherical Coordinates Calculus Volume 3




How To Solve This Question Integral E X X 2 1 X 1 2 Quora
Doubleintegralscalculator en Related Symbolab blog posts High School Math Solutions – Polynomial Long Division Calculator Polynomial longThe double improper integral ∫ − ∞ ∞ ∫ − ∞ ∞ e (− x 2 y 2 / 2) d y d x may be defined as the limit value of the double integrals ∬ D a e (− x 2 y 2 / 2) d A over disks D a of radii a centered at the origin, as a increases without bound;Double Integrals II Part 1 Iterated Double Integrals We begin by exploring the procedure your helper application uses to evaluate iterated double integrals You will find a discussion of this for your particular system in the worksheet In particular, we start with the integral of over the region bounded above by x = y 2 and below by y = x 2




Use Polar Coordinates To Evaluate The Double Integral Chegg Com



Faculty Nps Edu Pstanica Teaching Chap16 Sec8 9 Pdf
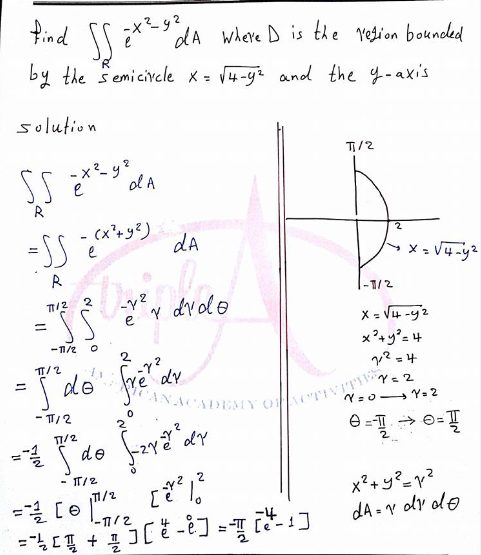
Practice problems on double integrals The problems below illustrate the kind of double integrals that frequently arise in probability applications The first group of questions asks to set up a double integral of a general function f(x,y) over a giving region$ \iint_D e^{x^2 y^2}\ dA $, where $ D $ is the region bounded by the semicircle $ x = \sqrt{4 y^2} $ and the yaxis ag Use a double integral to find the area of the region One loop of the rose $ r = \cos 3 \theta $ ag Alan G Numerade Educator 07 Problem 16 Use a double integral to find the area of the regionThat is, ∫ − ∞ ∞ ∫ − ∞ ∞ e (− x 2 y 2 / 2) d y d x = lim a




5 Double Integrals Over Rectangular Regions Pdf Free Download



2
R={(x,y)0 1 Educator answer eNotescom will help you with any book or any use a double integral to find the volume of the solid z= 4x^2 y^2 y= 2x 2 engineering maths double integral of f(x,y)dxdy in polar coordinates calculus evaluate the double integral ∫R∫ lny/x dA for the region R is the rectangle defined by 1 Calculus It's that edited for language e^x^2 which is a part of the integrand The obvious things to try, then, would be u = x 2 and u = e x 2 Another common trick is to swap the order of integration and hope you get something simpler out #4




Answered X Y E R X Y A 1 Andi Bartleby




Gaussian Integral Wikipedia
The double improper integral \int_{\infty}^{\infty} \int_{\infty}^{\infty} e^{x^{2}y^{2} / 2} d y d x may be defined as the limit value of the double integ Join our free STEM summer bootcamps taught by expertsWhen you are performing a double integral, if you wish to express the function and the bounds for the region in polar coordinates , the way to expand the tiny area is (Pay attention to the fact that the variable is part of this expression) Beyond that one rule, these double integrals are mostly about being careful to make sure the bounds of We should indeed use the polar coordinate system x=r cos phi y=r sin phi When you substitute these in x^2y^2, you get x^2y^2 = (r cos phi)^2 (r sin phi)^2 = r^2 cos^2 phi r^2 sin^2 phi = r^2 (cos^2 phi sin^2 phi) = r^2 for cos^2sin^2 = 1 Our area becomes 9




Example 2 Find Area Enclosed By Ellipse X2 Y2 B2 1



What Is The Integral Math Int X 2 E X 2 Dx Math Quora
Transform to polar coordinates See 153 Double Integrals in Polar Coordinates for a thorough guide mathx^2 y^2 = r^2, dxdy = r dr d\theta/math, and so you have math\displaystyle \int \int \sqrt{x^2 y^2} dx dy = \int \int \sqrt{r}^2Dx \) Solution to Example 2 The given integral cannot be easily calculated in rectangular coordinates hence the need to use polar coordinates instead522 Evaluate a double integral by computing an iterated integral over a region bounded by two vertical lines and two functions of x, x, or two horizontal lines and two functions of y y;




Calculus Homework Help And Exam Questions Page 2935




Calc3 1001 By James Bardo Issuu
The double integral \iint_D f (x,y) \, dA in rectangular coordinates can be converted to a double integral in polar coordinates as \iint_D f (r\cos (\theta), r\sin (\theta)) \, r \, dr \, d\theta\text {} 🔗 Example 1153 Let f (x,y) = e^ {x^2y^2} on the disk D = \ { (x,y) x^2 y^2 \leq 1\}\text {}The circle \({x^2} {y^2} = 4\) has the radius \(2\) and centre at the origin (Figure \(4\)) Figure 4 Since the upper half of the circle is equivalent to \(y = \sqrt {4 – {x^2}},\) the double integral can be written in the following form{eq}\int_0^{\sqrt 2} \int_{y^2}^2 y^3 e^{x^3}dxdy {/eq} Double Integrals When we have a double integral like the one above, where we really have no idea how to even begin to evaluate it,




Evaluate The Integral Double Integral R E Max X 2 Y 2 Da Where R 0 1 Times 0 1 And Max X 2 Y 2 Gives The Larger Of X 2 And Y 2 Study Com




Iterated Double Integral Multivariable Calculus Solved Past Paper Docsity
Evaluate the integral \\iint_{R^2} e^{10(x^2y^2)} \,dx \, dy \nonumber\ Solution This is an improper integral because we are integrating over an unbounded region \(R^2\) In polar coordinates, the entire plane \(R^2\) can be seen as \(0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty\) THeorem Double Integrals over Nonrectangular Regions Suppose g(x, y) is the extension to the rectangle R of the function f(x, y) defined on the regions D and R as shown in Figure 1521 inside R Then g(x, y) is integrable and we define the double integral of f(x, y) over D by ∬ D f(x, y)dA = ∬ R g(x, y)dAEvaluate the double integral e^x^2y^2 dA, where R is the region bounded by the semicircle x = square root(16y^2) and the yaxis Get more help from Chegg Solve it with our calculus problem solver and calculator




Gaussian Integral Wikipedia




Show How To Calculate The Iterated Integral Chegg Com
But this is a double integral, so if we switch the order of integration, we may be able to do something about this To switch the order, we will need to know the region The line in the graph is x= 3y Hence, if we are to switch the order of integration, xwill go from 0 to 3, and ywill be from 0 to x=3 Z 1 0 Z 3 3y ex2 dxdy= Z 3 0 Z x=3 0 ex2In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z)Integrals of a function of two variables over a region in (the realnumber plane) are called double integrals, and integrals of a function of three variables over a region in (realnumber 3D space) are called triple integralsThe question was math\displaystyle \int\int \dfrac{dx\;dy}{1 x^2 y^2}/math > ALERT THE SOLUTION IS NOT CORRECT, AS POINTED OUT BY SANSKAR > But, i don't like deleting answers Even, this might help somebody someday Here's your solutio




Double Integral Why Didn T The Author Substitute Y 4 Into X Sqrt Y Mathematics Stack Exchange



Math Wvu Edu Hlai2 Teaching Math251 Pdf Q7 Solution Pdf
1 Evaluate the double integral Z Z R 2xydxdy and R is bounded by y = x, y = 2 x and y = 0 Answer Z 1 0 Z 2 y y 2xydxdy = Z 1 0 (4y y2)dy = 2 3 2 Evaluate the double integral Z Z R e x2 y2 dxdy where R = f(x;y) 1 x2 y2 4g Answer Z 2ˇ 0 Z 2 1 re r2 drd = Z 2ˇ 0 1 2 e 4e 1 d = ˇ(e 1 e ) 3 Evaluate the double integral Z Z R q 16 x2Integrals » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for an integral integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;Er2rdrd = ˇ Z 2 r=0 rer2 dr = ˇ 2 er2j2 0 = ˇ 2 (e4 1) Find the volume of the solid inside the sphere x 2 y2 z = 16 and outside the cylinder x2 y2 = 4 Express this as twice the integral of the function z= p 16 x2 y2 over the xyplane Writing in polar coordinates makes the inner radius r= 2 (from x2 y2 22) and the outer radius r= 4 (so r2 = 16 and



2




Multiple Integral Wikipedia
First, the region D D is defined by, 0 ≤ θ ≤ 2 π 0 ≤ r ≤ 1 0 ≤ θ ≤ 2 π 0 ≤ r ≤ 1 In terms of polar coordinates the integral is then, ∬ D e x 2 y 2 d A = ∫ 2 π 0 ∫ 1 0 r e r 2 d r d θ ∬ D e x 2 y 2 d A = ∫ 0 2 π ∫ 0 1 r e r 2 d r d θ Notice that the addition of the r r gives us an integral Using Fubini's theorem, the above double integral can be seen as an area integral ∬ − a , a × − a , a e − ( x 2 y 2 ) d ( x , y ) , {\displaystyle \iint _{a,a\times a,a}e^{\left(x^{2}y^{2}\right)}\,d(x,y),}Upwards from z= 1 First, we write out the integral in Cartesian coordinates Note that the crosssections of the region in the xyplane are circles We can determine this by some algebra z= p 1 x2 y2 2 = p 1 x 2 y 4 = 1 x 2 y 3 = x 2 y So the largest circle (that sits on the plane z= 2) is given by the above formula, so the radius
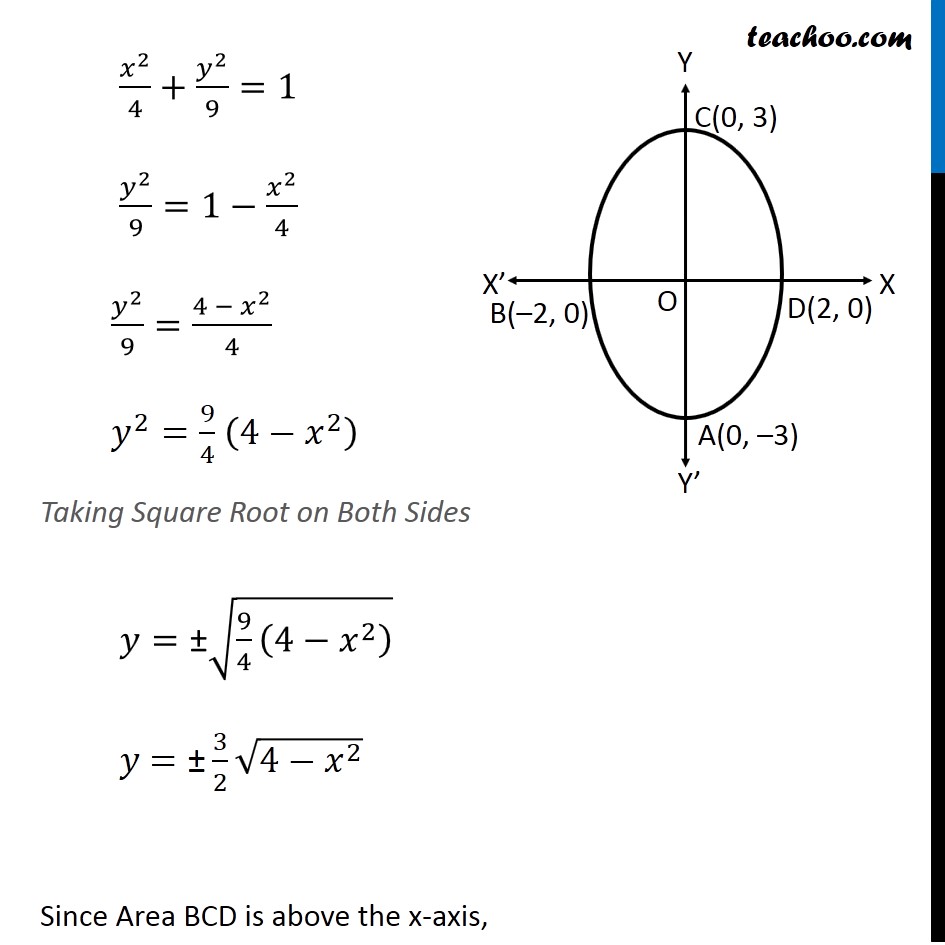



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12
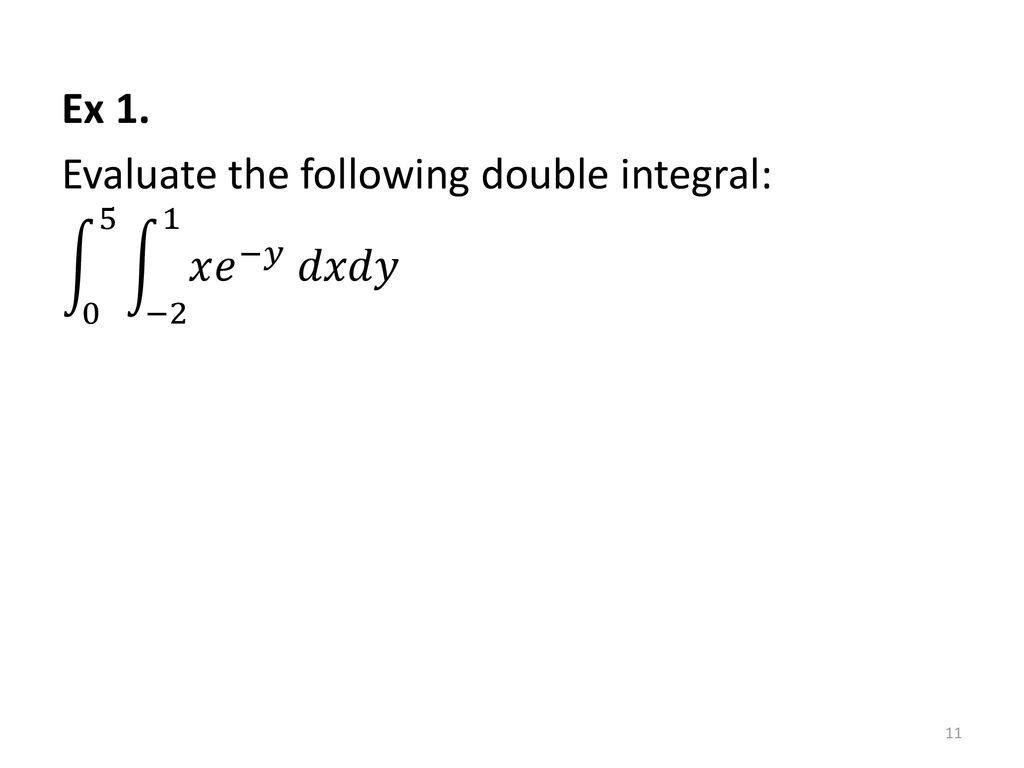



Math Double Integrals Ppt Download
523 Simplify the calculation of an iterated integral by changing the order of integrationProvided the limit exists Note The notation \(dA\) indicates a small element of area, without specifying any particular order for the variables \(x\) and \(y\text{;}\) it is shorter and more generic than writing \(dx\,dy\text{}\) We now capture our results from the earlier calculations using the notation of the double integral Theorem 412 Average Value of a Twovariable FunctionFollowing are some examples illustrating how to ask for double integrals int (x^2 y^2 x y^3) dx dy, x = 2 to 2, y = 2 to 2 integrate x^2 sin y dx dy, x = 01, y = 0pi



Evaluate E X 2 Y 2 Dxdy For X Y 0 0 By Changing To Polar Coordinates Sarthaks Econnect Largest Online Education Community



Verify Green S Theorem In The Plane For C Xy Y 2 Dx X 2dy Sarthaks Econnect Largest Online Education Community
Evaluate the double integral over the rectangular region Rdouble integration bounded region R (xy)/(sqrt(x^2y^21))dA ;A double integral is something of the form ZZ R f(x,y)dxdy where R is called the region of integration and is a region in the (x,y) plane The double integral gives us the volume under the surface z = f(x,y), just as a single integral gives the area under a curve 02 Evaluation of double integrals




Btech Ii Engineering Mathematics Unit3



2
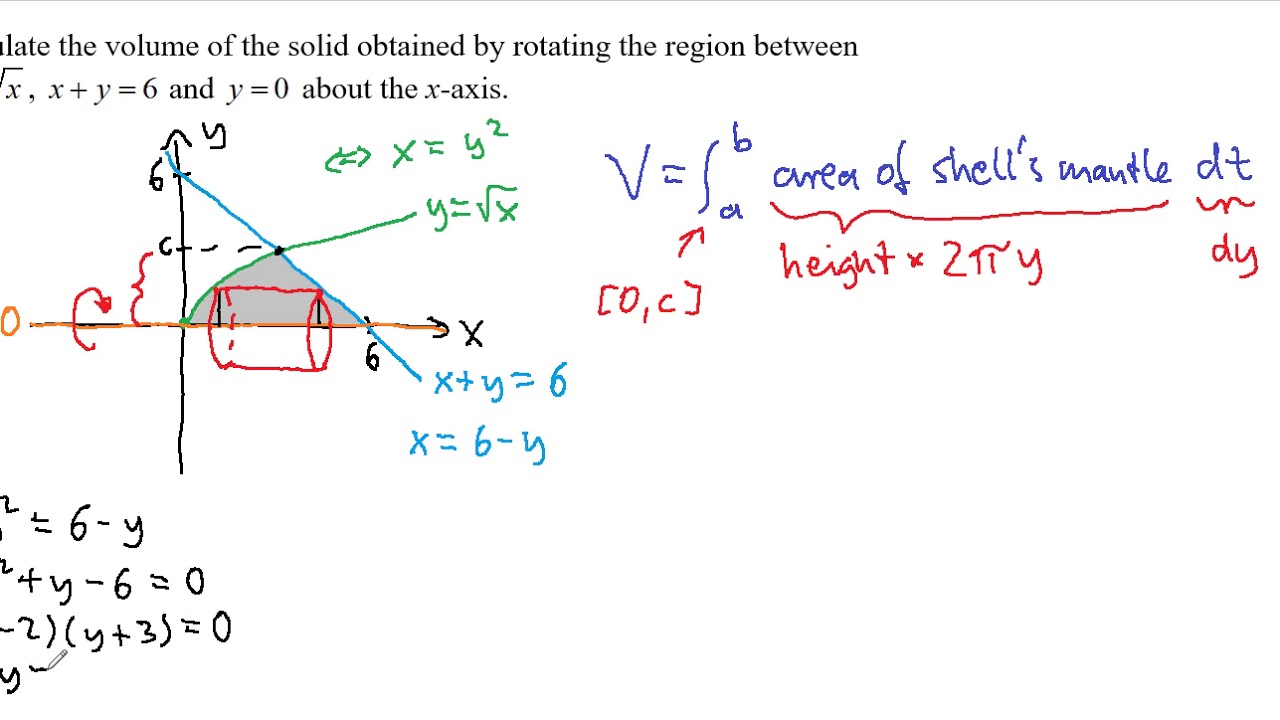



Volume Of Revolution Shell Method




Evaluate The Double Integral Of Exp X 2 Y 2 Where The Solid Is The Half Circle Given By X 2 Y 2 4 And X Y 0 Mathematics Stack Exchange




Double Integration



Docs Ufpr Br Roman Files Id5 Pdf



2



Examples Of Changing The Order Of Integration In Double Integrals Math Insight
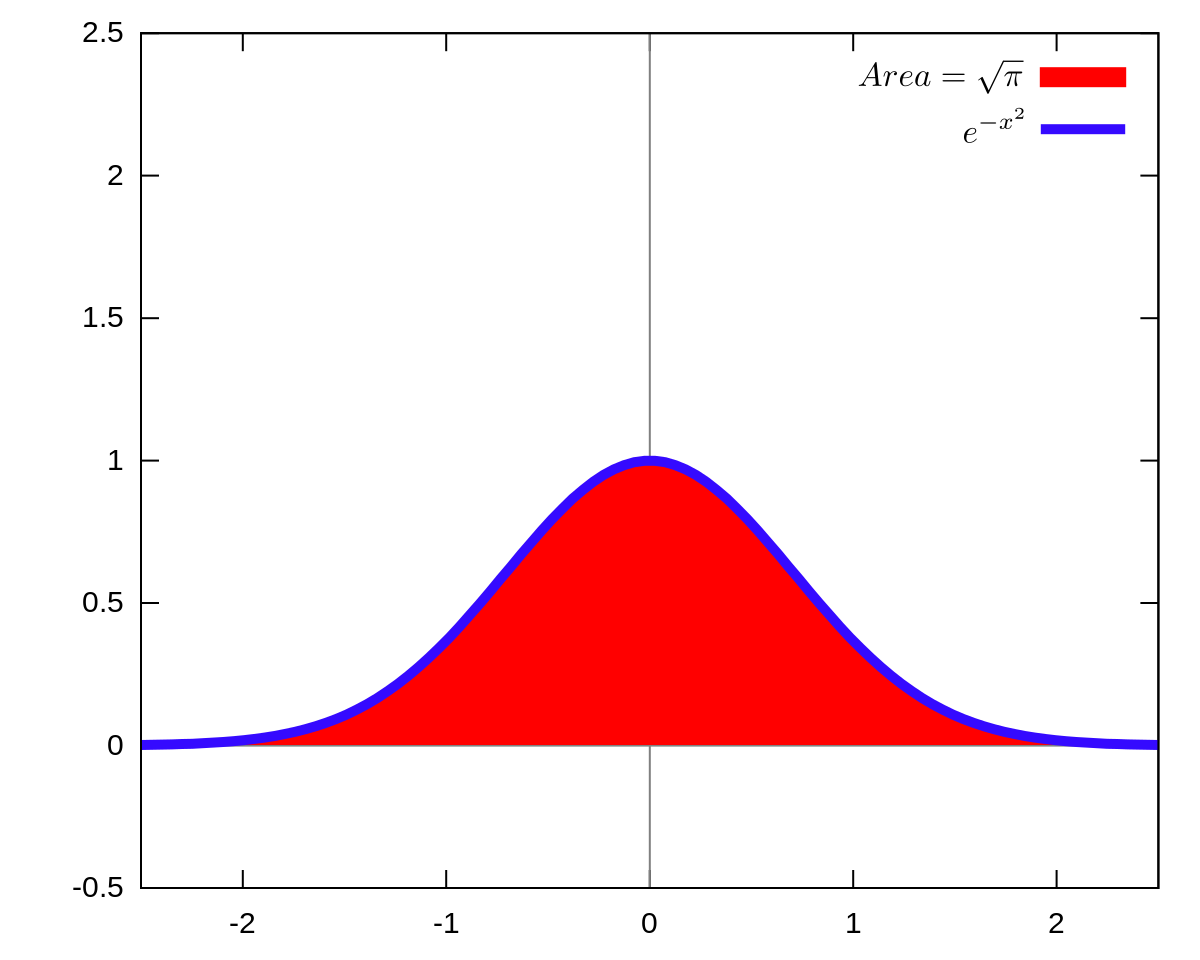



Gaussian Integral Wikipedia



Solved Set F X Y Vx2 Y2 And Consider The Double Integrals 1 F X Y Dady And J F X Y Dady Where D X Y 0 Lt Lt X2 2 Lt 1 An




Evaluate The Surface Integral Double Integral F Ds Where F E X Cos Yz X 2 Y Z 2 E 2x And S Is A Part Of Th Homeworklib



Web Northeastern Edu He Wang Teaching Teachingnotes Calculus3 Handout15 6 Pdf
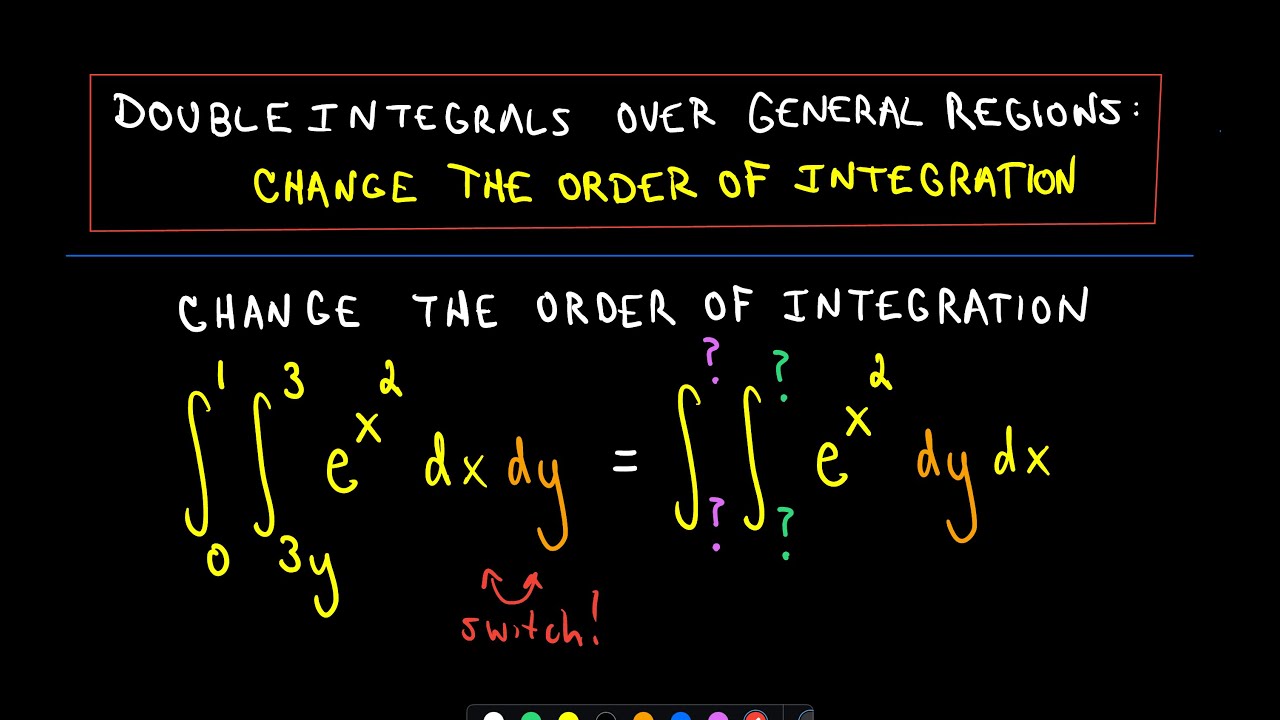



Double Integrals Changing Order Of Integration Full Ex Youtube




Double Integral E X Y 2 With Outer Limits 1 And 2 And Inner Limits 0 And Y 2 Brainly In




List Of Integrals Of Exponential Functions Wikipedia




How To Calculate Indefinite Integral Of Math E X 2 Math Quora




Definite Improper And Multiple Integration Stack Overflow




Evaluate The Iterated Integral Integral 1 2 Chegg Com
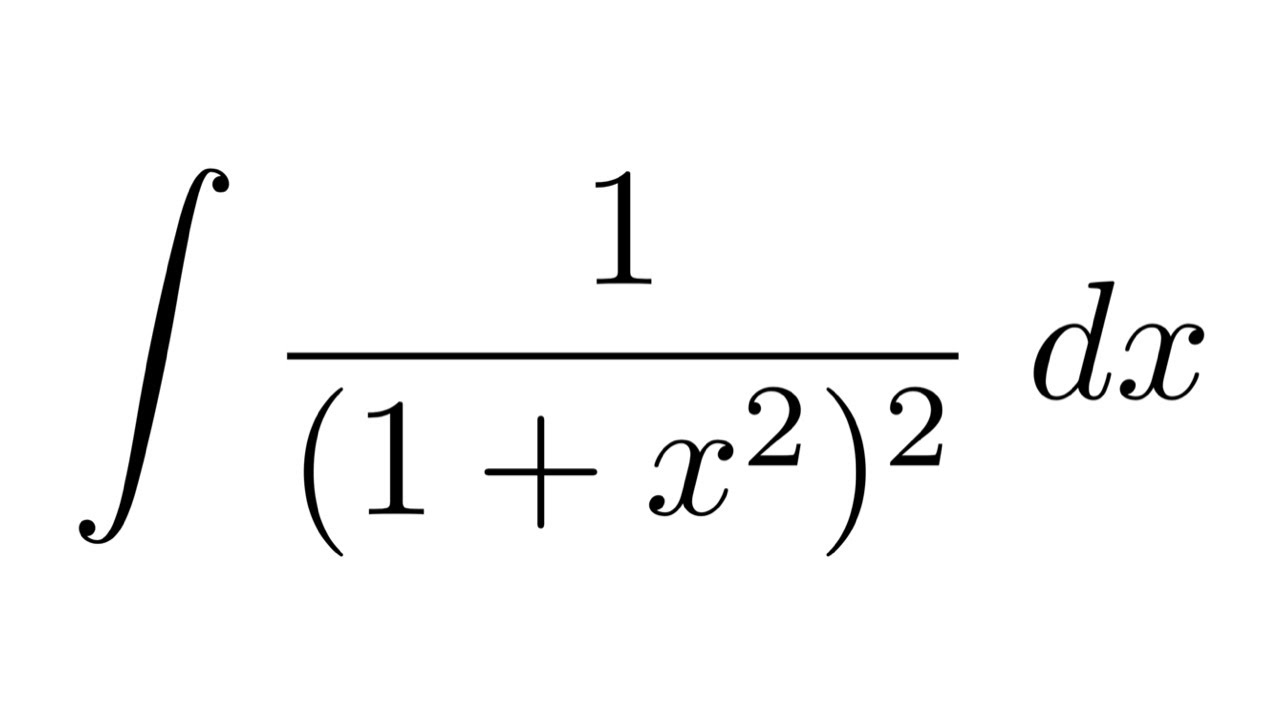



Integral Of 1 1 X 2 Substitution Youtube




Express Each Double Integral Over The Given Region R As An Iterated Integral Integral Triangle




Computing Integrals Springerlink



Www Jstor Org Stable



1



2




Double Integral



Can You Help Me With This Double Integral X 2 Y 2 Dxdy Where D X 2 Y 2 100 Quora




A Using Polar Coordinates Evaluate The Improper Chegg Com



1




Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download




Reverse The Order Of Integration And Evaluate Double Integral E Y 2 Dy Dx And Dy From 2x Homeworklib




Integral Calculator Integrate With Wolfram Alpha



What Is The Integral Of E X 4



2




Use Polar Coordinates To Evaluate The Double Integral Chegg Com




Calculate The Double Integral Iint R X Y 2 E X 2 Y 2 Dx Dy Where R Is The Square With Vertices 6 0 0 6 6 0 0 6 Study Com




Quiz 3 Solutions Multivariate Calculus Math 0 Docsity



How To Integrate X Sqrt X 2 Y 2 With An Order Dxdy Quora



2



2



1




Dan Kalman American University Ppt Download
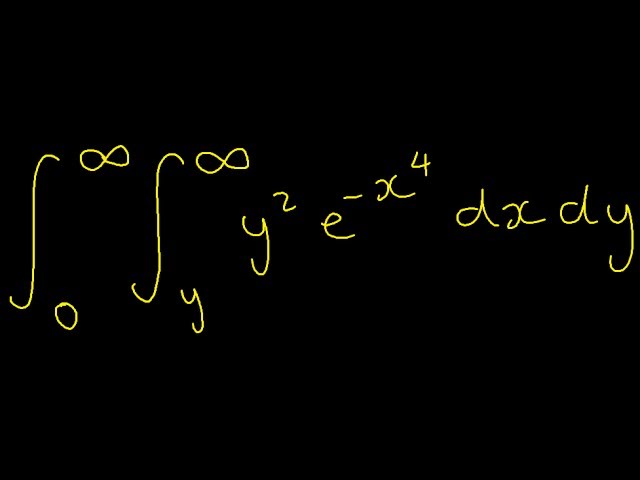



Double Integral Of Y 2 E X 4 Learnmathsfree Youtube




The Value Of The Integral Overset 1 Underset 0 Int E X 2 Dx L




Evaluate The Double Integral Sqrt X 2 Y 2 And Below The Sphere X 2 Y 2 Z 2 1 Youtube




If Y Ex Sin X Prove That D2y Dx2 2 Dy Dx 2y 0 Explain In Great Detail Mathematics Topperlearning Com 5p09j033




E Vs Exp In Display Mode Tex Latex Stack Exchange
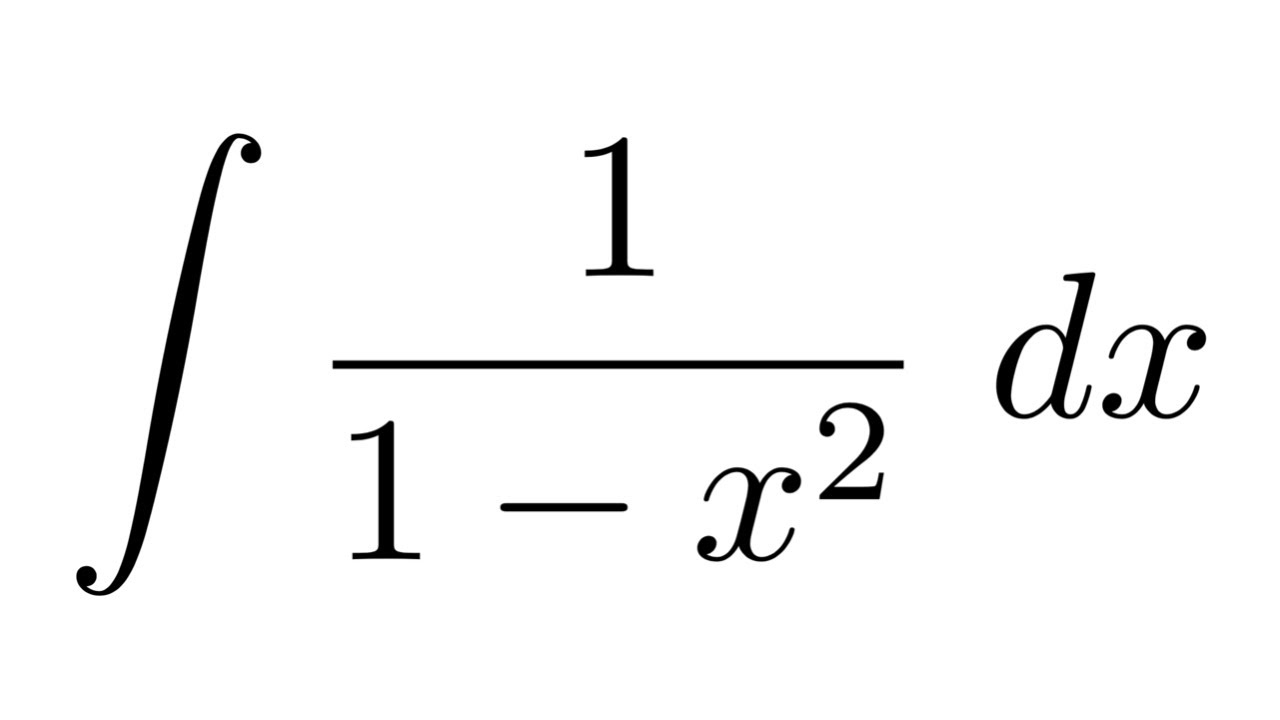



Integral Of 1 1 X 2 Substitution Youtube



1



Integral Rechnen Richtig Integral Von X 2 Y 2 1 4 X 2 Y 2 Dxdy Mathelounge




Lesson 19 Double Integrals Over General Regions



Multiple Integrals Calculus Early Transcendent
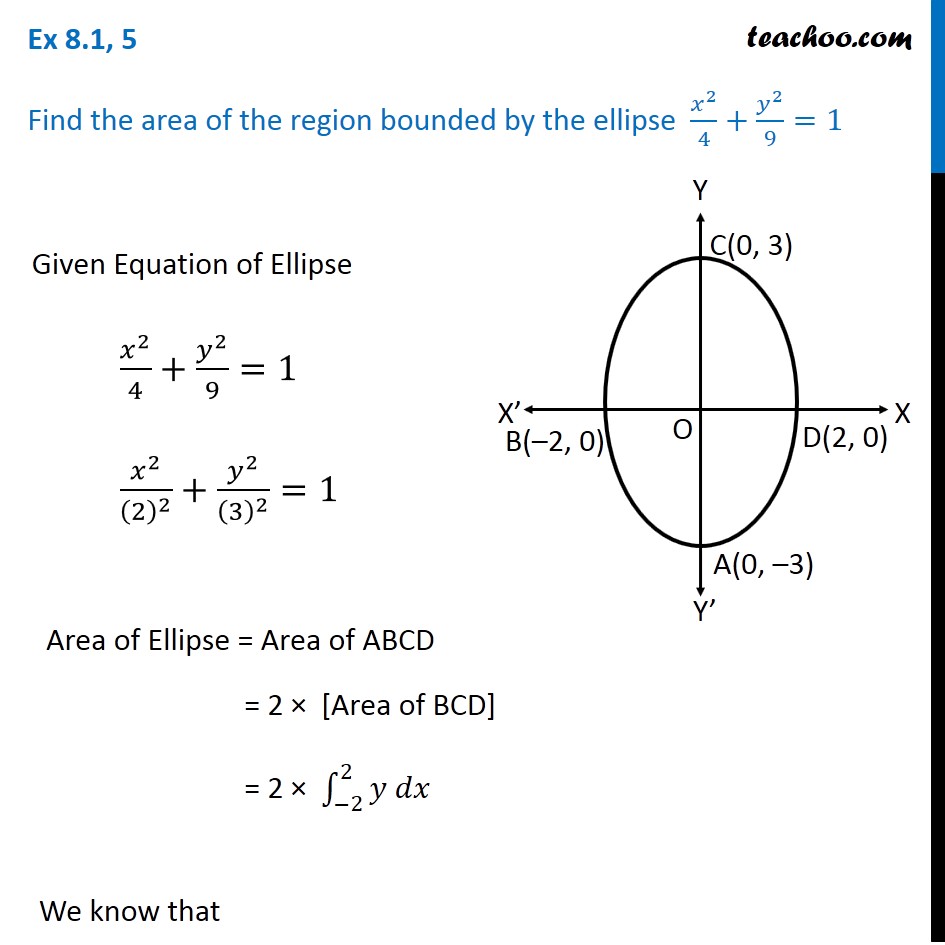



Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12




15 Multiple Integrals Multiple Integrals 15 3 Double
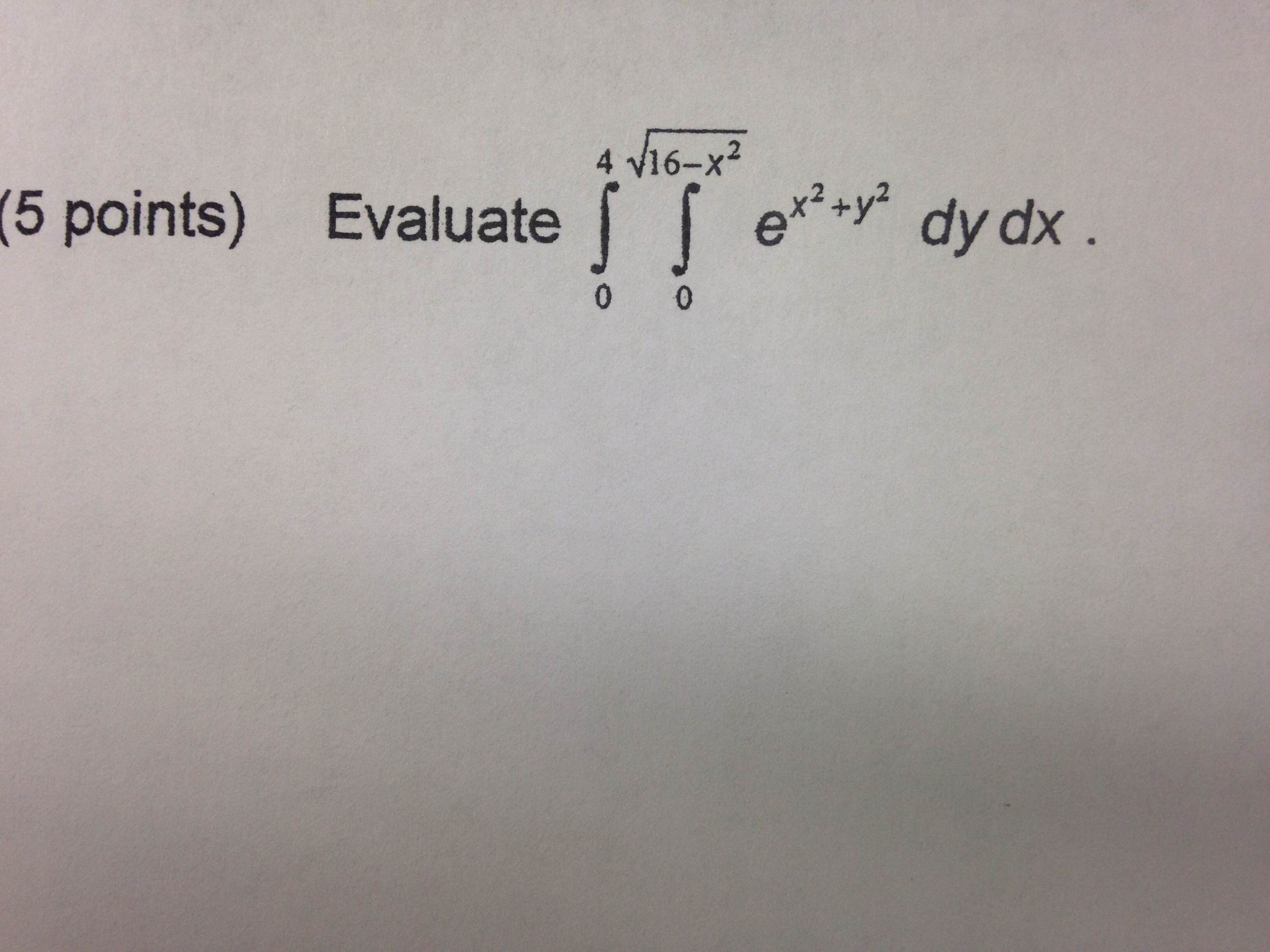



Evaluate Double Integrate E X 2 Y 2 Dydx Chegg Com




Gaussian Integral Wikipedia




Answered Express The Double Integral 1 X Da Bartleby



What Is The Complete Solution Of Double Integration Of Dx Dy 1 X2 Y2 Quora




Gaussian Integral Wikipedia




Compute The Following Double Integrals Sketch The Chegg Com



2




Evaluate The Integral Int 3 3 Int 0 Sqrt 9 X 2 E X 2 Y 2 Dy Dx Study Com




Document




Evaluate The Double Integral E X 2 Y 2 Da Where R Chegg Com



Calculate The Double Integral Int Int Xye X 2 Y Physics Forums




Consider Evaluating The Integral I Integral 2 Y 0 Chegg Com



Erf From Wolfram Mathworld




Evaluate The Given Integral By Changing To Polar Coordinates Double Integral E X 2 Y 2 Da Where D Is The Region That Lies To The Left Of The Y Axis Between The Circles X 2 Y 2




The Double Improper Integral E Dy Dx May Be Defined Chegg Com




Find The Particular Integral Of D 2 3d 2 Y E 3x



Http Web Iitd Ac In Siva Multiple Integrals Updated Pdf



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch16 Pdf




Consider The Improper Double Integral Integral Chegg Com




Evaluate The Double Integral Doubleintegral R Chegg Com




Several Variable Calculus




Ex 7 2 16 Integrate E 2x 3 Chapter 7 Class 12 Teachoo



I Would Like Help With This Double Integral E Problem Course Hero



2




Integrating Iint D 2xy Exp Y 2 Dxdy Over The Given Region Using Polar Coordinates Mathematics Stack Exchange




Volume Of Revolution Shell Method



Evaluating Double Integrals



0 件のコメント:
コメントを投稿